5. Trees and Tries
Table of Contents
A. General Introduction
I. Key Methods
- Identify the base case - what to do when it reaches the leaf or root node?
- Recursive calls to each child node
- Identify what needs to be calculated with the information from the child nodes
- Return the calculated result
II. Binary Search Tree (BST) Properties
- Inorder traversal gives the sorted order of the BST
- All values in left subtree are smaller than the current node
- All values in right subtree are larger than the current node
B. Leetcode problems
226. Invert Binary Tree
Given the root of a binary tree, invert the tree, and return its root.
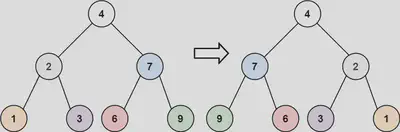
Key Ideas
- Invert the tree by swapping the left and right children of each node.
Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if root is None or root.left == None and root.right == None:
return root
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
543. Diameter of Binary Tree
Given the root of a binary tree, return the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
The length of a path between two nodes is represented by the number of edges between them.
Key Ideas
@BaseCaseThe diameter of an empty node is 0.@RecursiveCaseThe diameter of a node is the maximum of the diameter of its left and right subtrees.- Return the max height of the subtrees plus 1 (accounts for the edge that connects it to parent node).
code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
result = 0 # global state that is set at each level
def traverse(root:TreeNode):
if not root:
return 0
rh = traverse(root.right)
lh = traverse(root.left)
nonlocal result
result = max(result, rh+lh)
return max(lh, rh) + 1
traverse(root)
return result
104. Maximum Depth of Binary Tree
Given the root of a binary tree, return its maximum depth.
A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example:
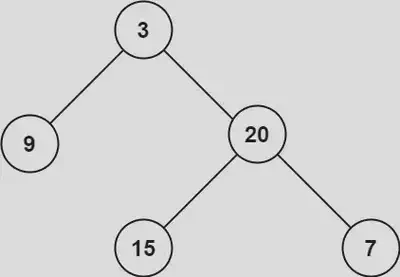
Input: root = [3,9,20,null,null,15,7]
Output: 3
Key Ideas
@BaseCaseThe depth of an empty node is 0.@RecursiveCaseCheck the max depth of right and left subtrees.- Return the max of the two plus 1 (To include the height of the current node).
code
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
depth = 0
if root.right:
rd = self.maxDepth(root.right)
depth = max(depth, rd)
if root.left:
ld = self.maxDepth(root.left)
depth = max(depth, ld)
return depth + 1
110. Balanced Binary Tree
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
Example:
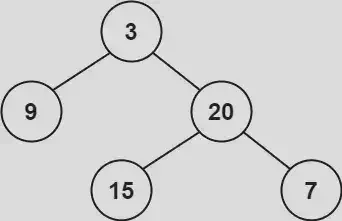
Input: root = [3,9,20,null,null,15,7]
Output: true
Key Ideas
@BaseCaseThe height of an empty node is zero.@RecursiveCaseThe height of a node is the maximum of the height of its left and right subtrees.- At every node, calculate if the difference in height between the left and right subtrees is greater than 1.
- If so, set the balanced set to false.
- Return the max height of the subtrees plus 1.
- At every node, calculate if the difference in height between the left and right subtrees is greater than 1.
code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
balanced = True
def dfs(root:TreeNode) -> int:
if root is None:
return 0
lh = dfs(root.left)
rh = dfs(root.right)
if abs(lh-rh) > 1:
nonlocal balanced
balanced = False
return max(lh, rh) + 1
dfs(root)
return balanced
100. Same Tree
Given the roots of two binary trees p and q, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
Example:
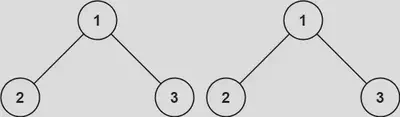
Input: p = [1,2,3], q = [1,2,3]
Output: true
Key Ideas
@BaseCaseIf both trees are empty, return true.@RecursiveCaseIf the trees are not empty, compare the values of the root nodes.- If they are not equal, return false.
- Otherwise, compare the left and right subtrees.
code
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
if not p and not q:
return True
if p and q and p.val == q.val:
l = self.isSameTree(p.left, q.left)
r = self.isSameTree(p.right, q.right)
if l and r:
return True
return False
572. Subtree of Another Tree
Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.
A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node’s descendants. The tree tree could also be considered as a subtree of itself.
Example:
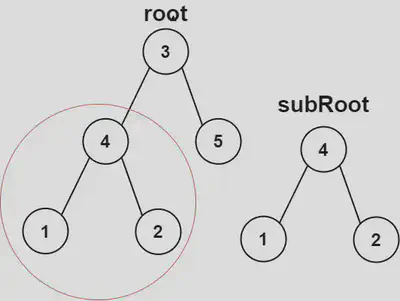
Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true
Key Ideas
- Use
isSameTreeto check the equality of the trees @BaseCaseIf root is empty, return false; because there is no subtree in an empty tree.@BaseCaseIf subRoot is empty, return true; because an empty subtree is a subtree of a tree with even one node@RecursiveCaseCheck if left subtree or right subtree is thesubRoot
Code
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
if not p and not q:
return True
if p and q and p.val == q.val:
l = self.isSameTree(p.left, q.left)
r = self.isSameTree(p.right, q.right)
if l and r:
return True
return False
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
if not root:
return False
if not subRoot:
return True
if self.isSameTree(root, subRoot):
return True
return self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)
102. Binary Tree Level Order Traversal
Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).
Example:
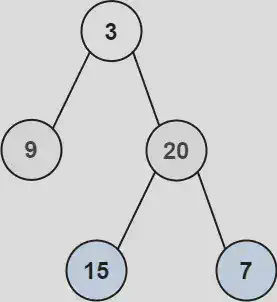
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]
Key Ideas
@BaseCaseIf the root is empty, return an empty list.- Used a multi-source BFS approach to traverse each level of the tree
code
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
result = []
queue = deque([root])
while queue:
layer = []
m = len(queue)
for _ in range(m):
node = queue.popleft()
layer.append(node.val)
# add children
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
result.append(layer)
return result
199. Binary Tree Right Side View
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example:
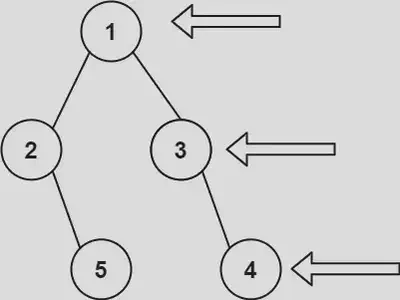
Input: root = [1,2,3,null,5,null,4]
Output: [1, 3, 4]
Key Ideas
@BaseCaseIf the root is empty, return an empty list.- Used a multi-source BFS approach to traverse each level of the tree
- for each level, have a value that is overwritten each node in the level
- At the end of the loop, the value would be the last node at the level
code
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
result = []
queue = deque([root])
while queue:
m = len(queue)
val = None
for _ in range(m):
node = queue.popleft()
val = node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
if val is not None:
result.append(val)
return result
1448. Count Good Nodes in Binary Tree
Given a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.
Return the number of good nodes in the binary tree.
Example:
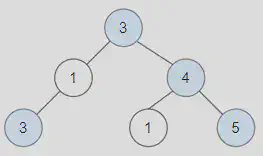
Input: root = [3,1,4,3,null,1,5]
Output: 4
Explanation: Nodes in blue are good.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path.
Node 3 -> (3,1,3) is the maximum value in the path.
Key Ideas:
@MainCasePass a maxval argument which is the maximum value in the path- If the current node’s value is greater than the maxval, then the node is good and the maxval is updated to the current node’s value
- Traverse the right and left subtrees
Code
class Solution:
def goodNodes(self, root: TreeNode) -> int:
if not root.left and not root.right:
return 1
result = 0
def dfs(root:TreeNode, maxval:int) -> None:
if root.val >= maxval:
nonlocal result
result += 1
maxval = root.val
if root.right:
dfs(root.right, maxval)
if root.left:
dfs(root.left, maxval)
dfs(root, root.val)
return result
98. Validate Binary Search Tree
Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- Both the left and right subtrees must also be binary search trees.
Example:
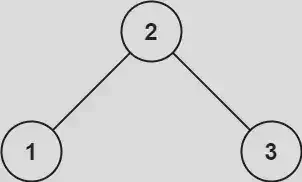
Input: root = [2,1,3]
Output: true
Key Ideas:
@BaseCaseIf the root is empty, return True.- Have a max and min value at each node; If the value of the node is greater than the max value, or less than the min value, then the tree is not a BST
- Check the left and right subtrees
code
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
if not root.right and not root.left:
return True
def dfs(root:TreeNode, maxval:float, minval:float):
if not root:
return True
if root.val >= maxval or root.val <= minval:
return False
r = dfs(root.right, maxval, root.val)
l = dfs(root.left, root.val, minval)
return r and l
result = dfs(root, float("inf"), float("-inf"))
return result
230. Kth Smallest Element in a BST
Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.
Example:
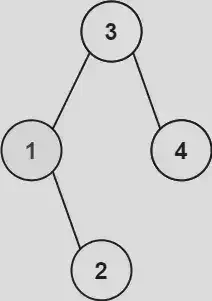
Input: root = [3,1,4,null,2], k = 1
Output: 1 \
Key Ideas:
- Traverse through the tree in order and return the kth value
- Return the
k-1th value as it is 1-indexed
code
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
heap = []
def traverse(root: TreeNode):
if not root:
return
if root.left:
traverse(root.left)
heap.append(root.val)
if root.right:
traverse(root.right)
traverse(root)
return heap[k-1]
105. Construct Binary Tree from Preorder and Inorder Traversal
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
Example:
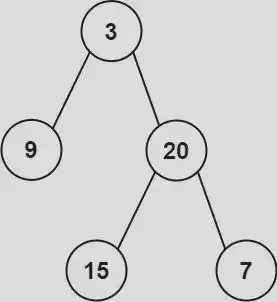
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
Key Ideas:
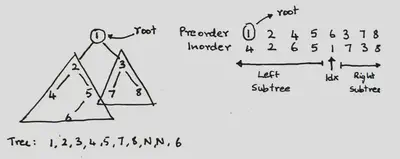
@BaseCaseIf the length of thepreorderandinorderis 0, return None- In
preorderthe first element is the root of the tree/subtree- Find the index of the root in
inorderand split thepreorderandinorderinto two subarrays - Recursively call the function on the subarrays
- Find the index of the root in
code
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if not preorder and not inorder:
return None
root = TreeNode(preorder[0])
rootIdx = inorder.index(preorder[0])
root.left = self.buildTree(preorder[1:rootIdx+1], inorder[:rootIdx])
root.right = self.buildTree(preorder[rootIdx+1:], inorder[rootIdx+1:])
return root
124. Binary Tree Maximum Path Sum
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node’s values in the path.
Given the root of a binary tree, return the maximum path sum of any non-empty path.
Example:
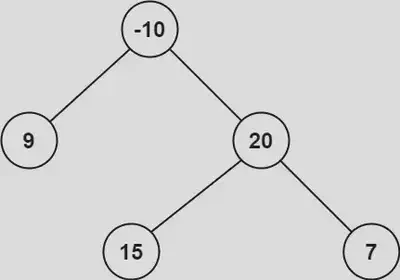
Input: root = [-10,9,20,null,null,15,7]
Output: 42 Explanation: 5 + 20 + 7 = 42
Key Ideas:
@BaseCaseIf the root is empty, return 0- The idea is very similar to finding diameter of a tree - we can find the maximum path sum of any path in the tree
- Initalize the max path with root value
- Traverse through the tree and at each node, the max value can be
maxvalueor<right-subtree-cost>+ root.val+<left-subtree-cost> - Return the sum of maximum of left and right subtree max values and the root value
Code
class Solution:
def maxPathSum(self, root: Optional[TreeNode]) -> int:
maxPathVal = root.val
if not root.left and not root.right:
return root.val
def dfs(root) -> None:
if not root:
return 0
lp = max(0, dfs(root.left))
rp = max(0, dfs(root.right))
nonlocal maxPathVal
maxPathVal = max(maxPathVal, lp+rp+root.val)
return max(lp,rp) + root.val
dfs(root)
return maxPathVal