6. Backtracking
Table of Contents
A. General Idea
The key intuition to understand backtracking is to imagine and formulize a problem as decision tree.
-
Define the base case for the decision tree; Base case determines the terminal condition of a path in a decision tree.
- Out of bounds
- Reach a target sum or value
-
Decide the actions to take in each node of the decision tree.
- Choose a candidate
- Prune the candidate
-
Maintain a global state to store the results
B. Leetcode problems
78. Subsets
Given an integer array nums of unique elements, return all possible subsets (the power set).
The solution set must not contain duplicate subsets. Return the solution in any order.
Example 1:
Input: [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
Key Ideas:
- The base case is when the index,
i, is out of bounds of the array.- Append the subset to result
- Action: Append a candidate at index
ito the subset and recursive call.- Prune the candidate at index
iand recursive call.
- Prune the candidate at index
code
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result = []
subset = []
def dfs(i):
if i >= len(nums): # base case - out of bounds
result.append(subset.copy())
return
subset.append(nums[i])
dfs(i+1)
subset.pop()
dfs(i+1)
dfs(0)
return result
90. Subsets II
Given an integer array nums that may contain duplicates, return all possible subsets (the power set).
The solution set must not contain duplicate subsets. Return the solution in any order.
Example 1:
Input: nums = [1,2,2]
Output: [[],[1],[1,2],[1,2,2],[2],[2,2]]
Key Ideas:
- The base logic is same as
78. subsetsproblem. - To handle duplicates, we sort the array to ensure duplicates are arranged consecutively.
- In the case of pruning, ensure to increment
itill the next element is different.- Why? This ensures that the right subtrees never contain the duplicate element.
- In the case of pruning, ensure to increment
code
from typing import List
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
result = []
m = len(nums)
# Algorithm:
# 1. Base case: idx >= len(nums): append to the result and return
# 2. Actions:
# 2.1 Include a number and call a recursive fn
# 2.2 Remove the number and call a recursive fn
nums.sort()
def generateSubsets(i,curr):
if i >= m:
result.append(curr.copy())
return
n = nums[i]
curr.append(n)
generateSubsets(i+1, curr)
curr.pop()
while i+1<m and nums[i] == nums[i+1]:
i += 1
generateSubsets(i+1, curr)
generateSubsets(0, []) # generate all the possible subsets without duplicates
return result
39. Combination Sum
Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.
The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.
It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.
Example 1:
Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]Explanation: 2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times. 7 is a candidate, and 7 = 7. These are the only two combinations.
Key Ideas:
-
There are multiple base cases for this problem
- when the sum of the array is greater than the target.
- when the sum of the array is equal to the target.
-
The action is to append a candidate to the current subset and recursive call.
- Prune the candidate and recursive call.
code
from typing import List
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
result = []
def dfs(decision_id:int, current_comb:List[int], current_sum:int):
# Identify and handle the base cases
if current_sum == target:
result.append(current_comb.copy())
return
if current_sum > target or decision_id >= len(candidates):
return
# Make the decisions and update the constraints
current_comb.append(candidates[decision_id])
dfs(decision_id, current_comb, current_sum + candidates[decision_id])
# Undo the decision and traverse another path
current_comb.pop()
dfs(decision_id+1, current_comb, current_sum)
dfs(0, [], 0)
return result
17. Letter Combinations of a Phone Number
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

Example 1:
Input: “23”
Output: [“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”]
Key Ideas:
- Base case is when the length of the combination is equal to the number of digits
- Generate a hashmap which maps the set of characters to the corresponding digit position
- Actions: Iterate through the set of character for a particular level and make a recursive call.
code
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
combinations = []
m = len(digits)
if m == 0:
return combinations
digits2char = {
"2":"abc",
"3":"def",
"4":"ghi",
"5":"jkl",
"6":"mno",
"7":"pqrs",
"8":"tuv",
"9":"wxyz",
}
chars = defaultdict(list)
for i, digit in enumerate(digits):
chars[i] = digits2char[digit]
def dfs(comb:str, level:int):
if len(comb) == m:
combinations.append(comb)
return
if len(comb) > m or level > m:
return
charsInLvl = chars[level]
for char in charsInLvl:
dfs(comb+char, level+1)
dfs("", 0)
return combinations
131. Palindrome Partitioning
Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.
A palindrome string is a string that reads the same backward as forward.
Example:
Input: s = “aab” Output: [[“a”,“a”,“b”],[“aa”,“b”]]
Key Ideas:
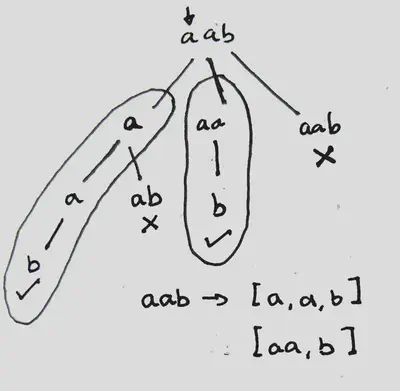
- Partition the string into substrings
- Check if the substring is a palindrome
- If it is, add it to current_partition, increment idx position in string and call the recursive function
- Pop the last element from current_partition
- If it is, add it to current_partition, increment idx position in string and call the recursive function
@BaseCaseIf the idx is greater or equal to the length of the string, add the current_partition to the result and return
code
class Solution:
def isPalindrome(self, s:str, l:int, r:int) -> bool:
"""Checks if a string is palindrome"""
while l<r:
if s[l] != s[r]:
return False
l += 1
r -= 1
return True
def partition(self, s: str) -> List[List[str]]:
if len(s) == 1:
return [[s]]
m = len(s)
result = []
current_partition = []
def traversePartition(idx:int):
"""Add palindrome partitions to result list"""
if idx >= m:
result.append(current_partition.copy())
return
for j in range(idx, m):
if self.isPalindrome(s, idx, j):
current_partition.append(s[idx:j+1])
traversePartition(j+1)
current_partition.pop()
# Exp Behav: Add palindrome partitions to the results
traversePartition(0)
return result
79. Word Search
Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example:
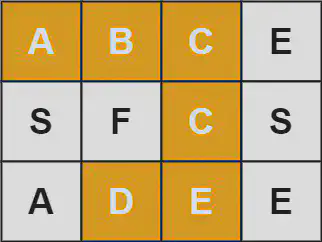
Input: board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
Output: true
Key Ideas:
@BaseCaseIf the current index is greater or equal to the length of the string, return true; That is we have found the entire word through traversal- Iterate through the neighboring cells and call the recursive function if the character at the current index is equal to the character at the current index in the string
code
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
m,n = len(board), len(board[0])
s = len(word)
DIRECTIONS = [(1,0), (0,1), (-1,0), (0,-1)]
check_boundaries = lambda x, y: x<m and x>=0 and y<n and y>=0
if s > m*n:
return False
def traverse(i, x, y):
if i >= len(word):
return True
for dx, dy in DIRECTIONS:
xx, yy = x+dx, y+dy
if check_boundaries(xx, yy) and board[xx][yy] == word[i]:
tmp = board[xx][yy]
board[xx][yy] = "#"
if traverse(i+1, xx, yy):
return True
board[xx][yy] = tmp
return False
for i in range(m):
for j in range(n):
if board[i][j] == word[0]:
board[i][j] = "#"
if traverse(1, i,j):
return True
board[i][j] = word[0]
return False
51. N-Queens
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example:
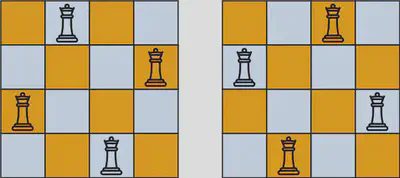
Input: n = 4
Output: [[".Q..","…Q",“Q…”,"..Q."],["..Q.",“Q…”,"…Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Key Ideas
-
@BaseCaseIf the current row equals the last row, then we have reached the end of the board and have successfully placed all the queens. -
The key idea is to identify that the negative diagonals follow the pattern
row-columnand the positive diagonals follow the patternrow+column. -
The basic intuition is to place each queen in each row. And then perform a brute-force search to find the correct column in each row.
-
Maintain three sets for each one of the following:
- Column
- Positive Diagonal
- Negative Diagonal
code
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
"""
Although the solution is bruteforce
"""
board = [["."]*n for _ in range(n)]
result = []
col = set()
posDiag = set()
negDiag = set()
def solveByRow(i:int):
if i == n:
solved = ["".join(row) for row in board]
result.append(solved)
return
for j in range(n):
if j in col or (i-j) in negDiag or (i+j) in posDiag:
continue
col.add(j)
negDiag.add((i-j))
posDiag.add((i+j))
board[i][j] = "Q"
solveByRow(i+1)
board[i][j] = "."
posDiag.remove((i+j))
negDiag.remove((i-j))
col.remove(j)
solveByRow(0)
return result
40. Combination Sum II
Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target.
Each number in candidates may only be used once in the combination.
Note: The solution set must not contain duplicate combinations.
Example:
Input: candidates = [10,1,2,7,6,1,5], target = 8
Output: [[1,1,6], [1,2,5], [1,7], [2,6]]
Key Ideas:
-
Sort the array so that duplicate numbers are next to each other
-
@BaseCasewhen the sum of the array is greater than the target. -
@BaseCasewhen the sum of the array is equal to the target. -
The action is to append a candidate to the current subset and recursive call.
- Prune the candidate and recursive call.
-
To handle duplicates, we sort the array to ensure duplicates are arranged consecutively.
- In the case of pruning, ensure to increment
itill the next element is different.- Why? This ensures that the right subtrees never contain the duplicate element.
- In the case of pruning, ensure to increment
code
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
result = []
candidates.sort()
def findComb(i:int, comb:List[int], total:int):
if total == target:
result.append(comb.copy())
return
if i >= len(candidates) or total > target:
return
c = candidates[i]
comb.append(c)
findComb(i+1, comb, total+c)
comb.pop()
while i < len(candidates)-1 and candidates[i] == candidates[i+1]:
i += 1
findComb(i+1, comb, total)
findComb(0, [], 0)
return result
46. Permutations
Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.
Example 1:
Inputs: nums = [1,2,3]
Outputs: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
Key Ideas
- It is more of bottom up approach of backtracking
- Keep spiltting the array into two parts and recursively call the function.
@BaseCaseWhen the length of the array is one, return the array as an array.
code
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
result = []
if len(nums) == 1:
return [nums.copy()]
for _ in range(len(nums)):
n = nums.pop(0)
perms = self.permute(nums)
for perm in perms:
perm.append(n)
result.extend(perms)
nums.append(n)
return result